تبسيط النظرية الخاصة لألبرت أينشتاين Albert Einstein الجزء الثاني
تحويلات لورنتز Lorentz transformation
عندما ظهر فشل النظريات الفيزيائية في الحالة السابقة بالنسبة للضوء , كان التفسير الأول أن هناك خطأ
في معادلات ماكسويل في الإلكتروديناميكا , التي كان يعود تاريخها إلى 20 عامًا فقط في تلك الفترة , و ظهر على ما يبدو
أن تلك المعادلات خاطئة , و لذلك كان لابد من تعديلها بحيث لا تتعارض تحويلات جاليليو مع مبدأ النسبية .
بناء على ذلك أضيفت حدود جديدة للمعادلات قادت للتنبؤ بظاهرة كهربية جديدة لم تكن موجودة مطلقًا أثناء
التجربة العملية , و لهذا كان لابد من التخلي عن هذه الطريقة .... و بالتدريج أصبح من الواضح أن معادلات ماكسويل
صحيحة ! , و أن الخطأ يكمن في مكان آخر .
في نفس الوقت كان العالم لورنتز Lorentz 18 July 1853 – 4
February 1928 - الحاصل على جائزة نوبل مشاركة مع بيتر زيمان Pieter Zeeman
25 May 1865 – 9 October 1943 – قد لاحظ شيئًا لافتاً للنظر و مثيرًا للفضول عندما
عوض بهذه القيم في معادلات ماكسويل
في معادلات ماكسويل في الإلكتروديناميكا , التي كان يعود تاريخها إلى 20 عامًا فقط في تلك الفترة , و ظهر على ما يبدو
أن تلك المعادلات خاطئة , و لذلك كان لابد من تعديلها بحيث لا تتعارض تحويلات جاليليو مع مبدأ النسبية .
بناء على ذلك أضيفت حدود جديدة للمعادلات قادت للتنبؤ بظاهرة كهربية جديدة لم تكن موجودة مطلقًا أثناء
التجربة العملية , و لهذا كان لابد من التخلي عن هذه الطريقة .... و بالتدريج أصبح من الواضح أن معادلات ماكسويل
صحيحة ! , و أن الخطأ يكمن في مكان آخر .
في نفس الوقت كان العالم لورنتز Lorentz 18 July 1853 – 4
February 1928 - الحاصل على جائزة نوبل مشاركة مع بيتر زيمان Pieter Zeeman
25 May 1865 – 9 October 1943 – قد لاحظ شيئًا لافتاً للنظر و مثيرًا للفضول عندما
عوض بهذه القيم في معادلات ماكسويل
و هذا يعني أن معادلات ماكسويل تبقى نفسها عندما نطبق هذه التحويلات . و عرفت المعادلات السابقة ب تحويلات لورنتز
Lorentz transformation .
و افترض أينشتاين , مستفيدًا من اقتراح Poincare Jules Henri
Poincaré - 29 April 1854 – 17 July 1912 – أنه حتى تبقى
القوانين الفيزيائية كما هي في تحويلات لورنتز , فإن ما يجب أن يتغير هو قوانين الميكانيكا و ليس قوانين الإلكتروديناميكا (
لن تتغير معادلات ماكسويل )
لقد بدا و كأن المتطلب الوحيد هو أن الكتلة m في معادلات نيوتن يجب أن تستبدل بالصيغة المذكورة في الجزء الأول
و عند إجراء هذا التعديل سوف تتوافق قوانين نيوتن و قوانين الإلكتروديناميكا , و عندها لو استخدمنا تحويلات لورنتز لمقارنة
قياسات Moe مع قياسات Joe فلن يكون بإمكاننا أن نكتشف أيهما متحرك لأن صيغ المعادلات ستصبح هي نفسها في نظامي
الإحداثيات . إنه من الممتع حقًا أن نناقش ما الذي يعنيه استبدال التحويلات القديمة بالإحداثيات و الزمن بالتحويلات الجديدة ؛
لأن التحويلات القديمة لجاليليو تبدو منطقية و بديهية أما تحويلات لورنتز فتبدو غريبة ! , و نحب أن نعرف أيها منطقية و
ممكنة عمليًا , و أيها ستكون الصحيحة . و لنصل إلى ذلك يجب أن نحلل مفاهيمنا عن الفراغ و الزمن من أجل أن نفهم هذه
التحويلات و حتى أن نصل إلى نتائج مقنعة , عندما تتفق النظرية مع التجربة .تجربة مايكلسون و مورلي
استمرت المحاولات لتحديد سرعة الأرض المطلقة خلال الوسط الافتراضي – الأثير – الذي يفترض أنه
يعم كل الفضاء . و أشهر هذه التجارب هي تجربة مايكلسون و مورلي سنة 1887 م , و بعد إجرائها بــ 18 عام تمكن
أينشتاين من تفسير نتائجها السلبية - حيث تساوت سرعة الضوء عند قياسها في اتجاهين متعامدين بالنسبة للأثير " المزعوم
" – فأنكر أينشتاين وجود الأثير .
تلخيص سريع لمبادئ النسبية الخاصة :
1 . تحافظ القوانين الفيزيائية ,سواء كانت ميكانيكية أو كهربية أو مغناطيسية أو ضوئية أو حتى معادلات ماكسويل –
المثيرة للجدل في ذلك الوقت - , على صورتها الرياضية في كل نظم المراجع القصورية – هياكل الإسناد
Reference framesأي التي تتحرك بسرعة منتظمة بالنسبة لبعضها . بعبارة أخرى " لا وجود للحركة
المطلقة " .
2 . سرعة الضوء في الفراغ لها دائمًا نفس القيمة بالنسبة لجميع المراجع القصورية بغض النظر عن سرعة المراجع بالنسبة
لبعضها , فسرعة الضوء لا تتغير بحركة الملاحظ أو حركة مصدر الضوء .
Lorentz transformation .
و افترض أينشتاين , مستفيدًا من اقتراح Poincare Jules Henri
Poincaré - 29 April 1854 – 17 July 1912 – أنه حتى تبقى
القوانين الفيزيائية كما هي في تحويلات لورنتز , فإن ما يجب أن يتغير هو قوانين الميكانيكا و ليس قوانين الإلكتروديناميكا (
لن تتغير معادلات ماكسويل )
لقد بدا و كأن المتطلب الوحيد هو أن الكتلة m في معادلات نيوتن يجب أن تستبدل بالصيغة المذكورة في الجزء الأول
و عند إجراء هذا التعديل سوف تتوافق قوانين نيوتن و قوانين الإلكتروديناميكا , و عندها لو استخدمنا تحويلات لورنتز لمقارنة
قياسات Moe مع قياسات Joe فلن يكون بإمكاننا أن نكتشف أيهما متحرك لأن صيغ المعادلات ستصبح هي نفسها في نظامي
الإحداثيات . إنه من الممتع حقًا أن نناقش ما الذي يعنيه استبدال التحويلات القديمة بالإحداثيات و الزمن بالتحويلات الجديدة ؛
لأن التحويلات القديمة لجاليليو تبدو منطقية و بديهية أما تحويلات لورنتز فتبدو غريبة ! , و نحب أن نعرف أيها منطقية و
ممكنة عمليًا , و أيها ستكون الصحيحة . و لنصل إلى ذلك يجب أن نحلل مفاهيمنا عن الفراغ و الزمن من أجل أن نفهم هذه
التحويلات و حتى أن نصل إلى نتائج مقنعة , عندما تتفق النظرية مع التجربة .تجربة مايكلسون و مورلي
استمرت المحاولات لتحديد سرعة الأرض المطلقة خلال الوسط الافتراضي – الأثير – الذي يفترض أنه
يعم كل الفضاء . و أشهر هذه التجارب هي تجربة مايكلسون و مورلي سنة 1887 م , و بعد إجرائها بــ 18 عام تمكن
أينشتاين من تفسير نتائجها السلبية - حيث تساوت سرعة الضوء عند قياسها في اتجاهين متعامدين بالنسبة للأثير " المزعوم
" – فأنكر أينشتاين وجود الأثير .
تلخيص سريع لمبادئ النسبية الخاصة :
1 . تحافظ القوانين الفيزيائية ,سواء كانت ميكانيكية أو كهربية أو مغناطيسية أو ضوئية أو حتى معادلات ماكسويل –
المثيرة للجدل في ذلك الوقت - , على صورتها الرياضية في كل نظم المراجع القصورية – هياكل الإسناد
Reference framesأي التي تتحرك بسرعة منتظمة بالنسبة لبعضها . بعبارة أخرى " لا وجود للحركة
المطلقة " .
2 . سرعة الضوء في الفراغ لها دائمًا نفس القيمة بالنسبة لجميع المراجع القصورية بغض النظر عن سرعة المراجع بالنسبة
لبعضها , فسرعة الضوء لا تتغير بحركة الملاحظ أو حركة مصدر الضوء .

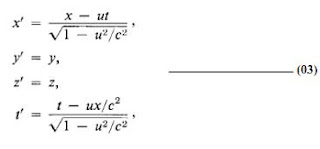




ليست هناك تعليقات: